为什么正态(高斯)分布在测试数据中如此常见?
正态分布(Normal distribution),也称高斯分布(Gaussian distribution)。
自然界最多的不是正态(高斯)分布,而是长尾(幂律等)分布。事实上,高斯分布更常见于人造体,而非自然界。
什么是正态分布?正态分布是一种概率分布。正态分布是具有两个参数μ和σ2的连续型随机变量的分布,第一参数μ是遵从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差,所以正态分布记作N(μ,σ2 )。
正态分布怎么来的?只要你观察的系统里,各种对象之间关联很弱,那么它们的总和平均表现,根据中心极限定理,就是正态或者近正态的。如看我们的测试机和芯片,它们都是我们人造的东西,基本都是模块化的,一个模块和另一个模块之间关联很弱,坏了一个模块换掉就好。所以人造系统,其表现,包括性能,稳定度都基于正态分布。
那么什么是中心极限定理?中心极限定理说明的是在一定条件下,大量独立随机变量的平均数是以正态分布为极限的。顺便说下,不要把大数定律和极限中心定理弄混。大数定律和中心极限定理的区别在于,大数定律揭示了大量随机变量的平均结果,但没有涉及到随机变量的分布的问题。
正态分布是误差理论的基石,我们实际生活中绝大部分情况下遇到的正态分布,都来源于大量随机变量的累加,而中心极限定理保证了这一切的和都会近似成一个正态分布。从测试机的测试稳定性到产品的参数的分布,我们不难从极限中心定理去理解,为什么我们在对同一颗产品进行重复测试时呈现的分布通常是正太分布(不考虑芯片发热等其他外在因素影响)。因为它服从测试机的误差,而测试机的误差是测试机内部各个模块的随机误差导致的。每次的重复测试都是这些模块的随机误差在起作用,也就是我们每次是在去它们的误差和或平均来得出测试结果。所以也就不难理解我们的重复测试的结果是正太分布的。 然后我们在放眼测试产品本身,产品本身是经过各种工艺而最后形成的产物,而各种工艺或机器也可以认为是相互对立的模块,他们对产品导致的误差的分布也是符合正态分布的。
下面举一个实例,大家可以用EXCEL随机生产一组数据(如附件 uyu,1-100),我们可以看出“随机结果的分布”的分布图(其中x轴1代表0-10,2代表10-20,以此类推)。可以看出随机的结果是相对平均的。然后我们将数据随机的取10个来做平均,然后我们在看它的平均数分布,我们不难看出平均值的分布已经成了正太分布了。
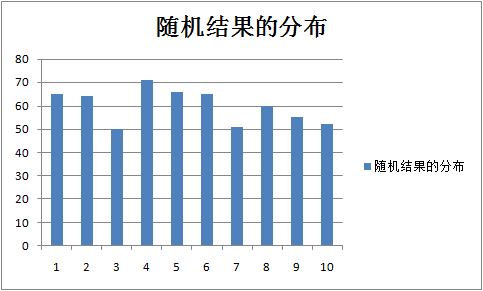
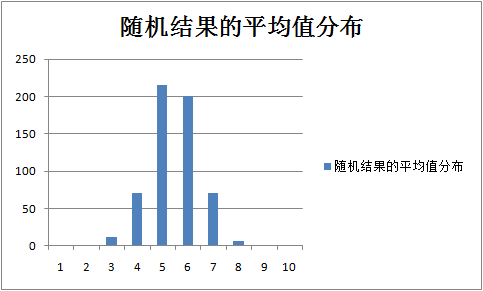
正太分布对于我们测试的意义很大,不仅仅在数据分析中,在对于我们的各行各业的各种问题分析和质量管控起到了很大的作用。如6sigma,GRR,TCS 等等都是基于正态分布的基础上进行分析的。了解什么是正太分布,为什么正态分布,对于我们在分析基于正太分布而形成的理论和应用时,我们就可以做到知其然而知其所以然。
本文地址: http://www.kanwoda.com/blog/archives/09231603131374.html