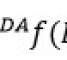数据与质量 —TCS的秘密(快速搞定GuardBand）

TCS -Test Capability Study，是更为简单的方法得出 Guardband 以及GRR%的好方法。可以理解为简化的GRR。TCS 和GRR的主要区别是TCS省去了DUT的复测。

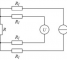
TCS的需求和setup方式通常和GRR差不多。要求如下：

2套以上的板子，2套以上测试系统，一定数量的DUT，通常规定setup的数量要达到30以上。也就是说，根据不同的测试site的数量，我们可以灵活的选择DUT的数量，不过DUT的数量一定要比Site的数量多些。

Setup的方式：例如8个site，16个DUT。就是DUT1Site1 – DUT8Site8，DUT2Site1 – DUT9SITE8 … DUT16SITE1 – DUT7SITE8，每个setup就只要测试一次。这就是我们需要收集的数据，是不是比GRR更为简单和方便？而且也避免了重复测试（repeat）时的DUT自身加热导致的误差。

那么问题来了，为什么我们可以这样做？我们不需要考虑重复测试的误差吗？

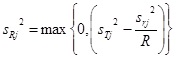我们知道测试的误差主要来自于2个方面，一个是系统误差，一个是重复测量误差，可以表达为：M=T+Es+Er (其中M代表我们测试的结果，T代表DUT的真实值，Es也就是系统误差也就是GRR里的reproducibility 误差，Er重复测试性误差也叫随机性误差）。GRR的做法是把二者分开分析，然后在算出各自的standard Deviation后，再结合在一起得出参数x的整体Sx。而TCS呢？因为每次测试实际上都包含了2种误差，所以TCS是将2者放在一起来分析的。留心的朋友会注意到，我们在GRR 计算是有把因为repeatiability引起的standard deviation减去，所以2者是独立的分析。

那么TCS的方差怎么计算呢？很简单，可以参考GRR的整体步骤，只是不用考虑repeatability的方差也不用减去repeatiability的方差。我们来看看为什么TCS可以和GRR一样得出正确的GuardBand 和GRR%呢。

我们知道GRR和TCS一样都是方差分析法，GRR的参数m的standard deviation的平方等于Var(X)+Var(Y)。(其中Var就是方差的意思(variance)，X我们当做reproducibility的方差变量，Y当做repeatiability的方差变量，Var(X),Var(Y) 就是变量X,和变量Y的标准方差的平方)。TCS的参数m的standard deviation的平方我们可以写成Var(X+Y)。可以分析得出Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)，Cov(X,Y) 为协方差。对于独立的正太分布的变量X和Y来说，Cov(X,Y)=0；我们也就可以得出Var(X+Y)=Var(X)+Var(Y)。所以TCS的分析结果和GRR的是一致的。

那么GRR的好处又是什么呢？GRR可以单独把repeatiablity的方差分析出来，如果Guardband不够理想，我们可以比较清楚的看出是那个方差导致的，比较容易分析问题。

不知道有没有人想过为什么Guardband的计算用的是3倍的standard deviation，为什么我们一直强调setup的数量？3倍的原因是：根据分析在一个CPk为0.67的正太分布的数据(一半的1.33cpk, robust data)，用3倍的standard deviation计算出的Test Escape 为14ppm,(1倍为930ppm,2倍的为116ppm)，可想而知，当CPK越大，可能test escape的ppm会越小。根据经验和正太数据分析当取3倍的standard deviation作为guard band时，平均的失效率≦3.4ppm。如果取太大的倍数的standard deviation会造成yield loss，所以3倍是比较合适的数值。而setup数量，这是因为我们真实的standard deviation（另一个名者叫Sigma，也就是全体样本的standard deviation） 需要一定的自由度（setup 数量-1）才能根据sample standard deviation得出一个比较紧凑的sigma分布区间。比如如果我们setup的数量为4，那么在置信区间95%，sigma的分布范围为0.566*S_sample-3.729*S_sample。虽然我们在最终的S用了矫正因子C4，但是如果setup数量不足也会影响GB的准确性。
本文地址: http://www.kanwoda.com/blog/archives/0522291014509.html

+191