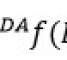Propagation Of Error(POE) 分析方法

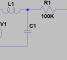
如果有客户问你“你的产品规范规定VFB（基准电压1V）是+/-2%，我用的电阻是1%的，那么我的VOUT(5V）的输出范围是多少？”。你会如何回答客户呢？

员工甲可能回答”根据最坏的情况（Worse Case Analysis),Vout(Vout=(R1+R2)/R1*VFB,其中R2=4R1) 的范围是
Vout1=(1+R2*0.99/R1*1.01）*（VFB*0.98） 到 Vout2=(1+R2*1.01/R1*0.99）*（VFB*1.02）.Vout1=96.45%*Vout_target到Vout2=103.65%*Vout_target 就是它的范围。”

员工乙马上插嘴”客户的需求是+/-3%.”我们会因为不够精确的分析方法导致客户的流失。

什么是POE？假如我们一个参数体积V=L*W*H. L,W,H都是固定值，那么V也就没有误差了。

现在我们假定L和W是固定的，那么ΔV=∂V/∂H*ΔH,也就是说ΔH的变化会形成∂V/∂H（这里是L*W)倍的ΔH的ΔV变化。

如果一关系式F=F(a,b,c..),a,b,c..都是变化的变量。

那么ΔF≈∂F/∂a*Δa+∂F/∂b*Δb+∂F/∂c*Δc…

因此体积ΔV=∂V/∂L*ΔL+∂V/∂W*ΔW+∂V/∂H*ΔH 如果L,W,H都为变量的话。

如果用方差的方式来表示变量的变化范围，那么ΔL，ΔW，ΔH,可以表示为σl^2  (Var(ΔL)),σw^2  (Var(ΔW)),,σh^2 (Var(ΔH))。

V的方差表达式：σv^2=(∂V/∂L)^2*σl^2+(∂V/∂W)^2*σw^2+∂V/∂H*σh^2。

推导如下：

Var(ΔV)=σv^2=Var(∂V/∂L*ΔL+∂V/∂W*ΔW+∂V/∂H*ΔH )

=Var(∂V/∂L*ΔL)+Var(∂V/∂W*ΔW)+Var(∂V/∂H*ΔH)

=(∂V/∂L)^2*Var(ΔL)+(∂V/∂W)^2*Var(ΔW)+∂V/∂H*Var(ΔH)

=(∂V/∂L)^2*σl^2+(∂V/∂W)^2*σw^2+∂V/∂H*σh^2

用方差的表达方式更利于统计学的分析。下面我们来做个实例。

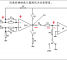
我们就以上面碰到的问题来分析。Worse Case不能很好的表达统计学上Vout的分布范围。假设VFB和电阻R1,R2的CPK都为1.33，我们知道Vout=(R1+R2)/R1*VFB，那么σvout^2=(∂Vout/∂R1)^2*σR1^2+(∂Vout/∂R2)^2*σR2^2+(∂Vout/∂Vfb)^2*σvfb^2. CPK=1.33的意思4σ的范围就是它生产控制的范围。如电阻R1的4σR1的范围就是1%*R1，4σVfb的范围就是2%*VFB。

∂Vout/∂R1=R2/R1^2*VFB,

∂Vout/∂R2=1/R1*VFB,

∂Vout/∂Vfb=(R1+R2)/R1,

σvout^2=(∂Vout/∂R1)^2*σR1^2+(∂Vout/∂R2)^2*σR2^2+(∂Vout/∂Vfb)^2*σvfb^2

=(R2/R1^2*VFB)^2*(1%R1/4)^2+(1/R1*VFB)^2*(1%R2/4)^2+((R1+R2)/R1)^2*(2%*VFB/4)^2

=0.574%

实际上 Vout的变化小于变量变化范围的平方和的平方根，如果当R2远大于R1时，Vout的变化就是所有相关变量的平方和的根了。

经以上计算可以得出Vout的4σ变化范围为+/-2.297%.该范围的CPK和Vfb和电阻的一致，为1.33.如果Vfb的和电阻的CPK更好Vout的CPK也会更好。

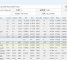
同样我们也可以用excel跑一个Monte Carlo，来看看我们的结果对不对。Monte Carlo的sample数量越多越接近我们POE的值。详细结果请看附件POE。(蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。)

 
本文地址: http://www.kanwoda.com/blog/archives/0712143926670.html

+193