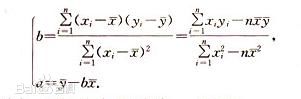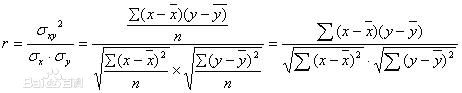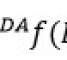线性回归分析（Linear Regression Analysis）在测试中的应用

线性回归是利用统计学中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。分析按照自变量和应变量之间的关系类型，可分为线性回归分析和非线性回归分析。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

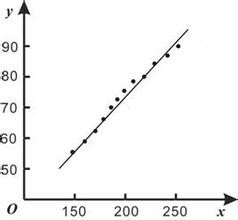
在测试分析中通常应用的是一元或多元线性回归分析。线性回归分析的拟合线 的公式可以表达为y=ax+b，其中还有相关系数r来表达拟合度。

在EXCEL中我们可以简单的针对1组或几组数据进行分析。附件为参考数据和方法(Regression)。EXCEL也自带拟合线的计算和R值得计算。

步骤如下：1、将数据输入excel表格中，行表示或列表示均可。2、选定数据区域，然后单击工具栏中的“图表向导”(弹出对话框，选择“xy散点图”，再选择子图表中的第一个散点图。3、按“下一步”，大概的图就完成了，它会让你选择所产生的数据是“行”或“列”，根据你的要求选择。再点击下一步，可以将行或列的标题内容填入。接着点击“下一步”之后点“完成”。图表就完成了。4、选择图表上的任意一个点（选中一个点之后，其余的点都变为黄色了），单击右键，选择“添加趋势线”。在“添加趋势线”对话框中的“类型”选“线性”，在“选项”中把“显示公式”和“显示R平方值”点上。

拟合的线性方程中，,

相关系数r越接近1证明相关性越好，通常r的平方大于0.9时，就认为相关性就不错了。当然这也不是绝对的，具体问题具体分析。如果是x和y的数组是一样的，那么相关系数r=1.

在测试中的分析及应用是很多的，如在参数在不同温度下的相关性,根据公式及相关性可以我们可以根据参数值推导出温度，也可以根据常温的参数推导出高温的参数值。

或者如lot前后2次测试的相关性，有时我们需要验证参数在经历过一些over stress或者Qualification 等等一些验证过后，看数据或参数是否发生了变化，我们也可以用线性回归来分析。

或者如某些参数之间的相关性，有些参数会在device被burn前被测试，被burn后同样测一遍，我们就可以通过线性回归的分析来分析前后的差别。

或者用来做Correlation，比如有些产品我们需要转移到其他工厂，需要验证在转移过程中没有问题，这时可以用线性回归的方法来对比2边的测试数据。

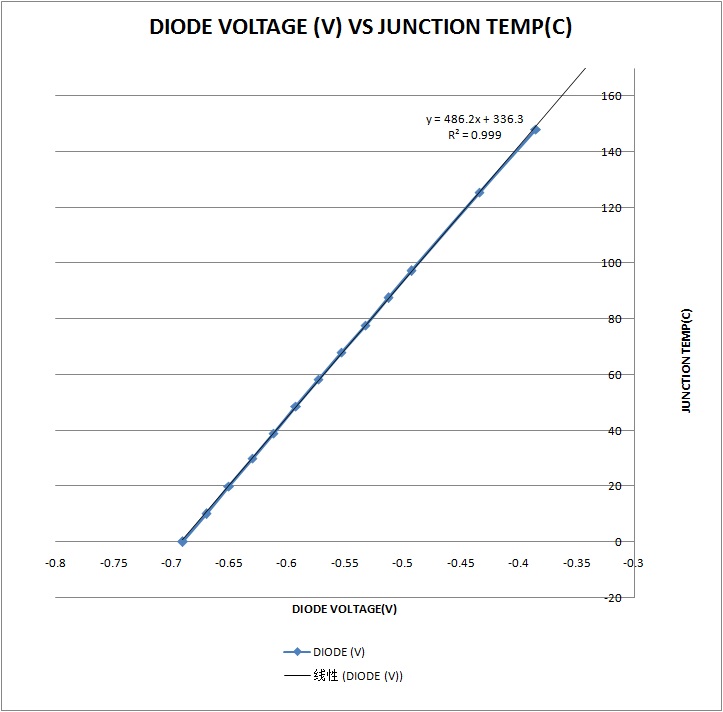
应用的场景很多。下面简单介绍一个实例，测试芯片中二极管的电压和温度的相关性。在一些公司中会利用到通过二极管来感应 junction temp。

从下图我们可以看出，device的junction temp和 diode voltage 相关系数R非常接近于1，证明这二者之间的相关性非常好。这样我们就可以在测试中通过关系式y=486.2x+336.3很轻易的得出当前产品的温度，其中x为diode的导通电压。

 
本文地址: http://www.kanwoda.com/blog/archives/08152006151219.html

+459